What is approximation error?
Approximation error in some data is the discrepancy between an exact value and some approximation to it. An approximation error can occur because:
- The measurement of the data is not precise due to the instruments. (e.g., the accurate reading of a piece of paper is 4.5 cm but since the ruler does not use decimals, you round it to 5 cm.) or
- Approximations
In the mathematical field of numerical analysis, the numerical stability of an algorithm indicates how the error is propagated by the algorithm.
One commonly distinguishes between the relative error and the absolute error.
Given some value v and its approximation approx, the absolute error is;
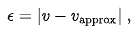
Where, the vertical bars denote the absolute value. If v =/= 0, the relative error is;
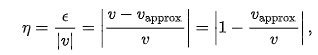
And, the percent error is
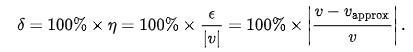
In other words, the absolute error is the magnitude of the difference between the exact value and the approximation. The relative error is the absolute error divided by the magnitude of the exact value. The percent error is the relative error expressed in terms of per 100.
An error bound is an upper limit on the relative or absolute size of an approximation error.
How to calculate approximation error?
There are two main ways to gauge how accurate is an estimated error of the actual (not precisely know) value x:
- The absolute approximation error that’s defined as |xe − x|, and
- The relative approximation error that’s usually defined as the ratio of the absolute error and the actual value:
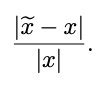
Since the actual value x is now known exactly, we cannot compute the exact values of the corresponding errors. Often, however, we know the upper bounds on one of these errors (or on both of them). Such an upper bound serves as a description of approximation accuracy: we can say that we have an approximation with an accuracy of ±0.1, or with an accuracy of 5%.
The problem with the usual definition of a relative error
When the actual value is positive or negative, relative error makes perfect sense: the smaller the relative error, the close the estimate xe to the actual value x. However, in a 1 frequent situation when the actual value is 0, the relative error does not make sense: no matter how close is our estimate xe to 0, the relative error is infinite.
It is therefore desirable to come up with a more adequate relative description of approximation error. A new definition of the relative error: a suggestion. We propose, when defining relative error, to divide the absolute error not by the actual (not precisely known) value x, but rather by the approximate (known) value xe. In other words, we propose the following new definition of the relative approximation error:
.
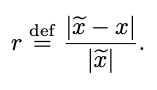
An argument in favor of the new definition. With this new definition, if we know the approximate estimate xe, and we know the upper bound δ on the relative error r, we can conclude that the actual value x is somewhere between xe − δ · xe and xe + δ · xe.
For example, if we have an approximate value 2, and we know that the relative error is no more than 5%, then in this new definition this would simply mean that the actual value is somewhere between 2 − 0.05 · 2 = 1.9 and 2 + 0.05 · 2 = 2.1.
In contrast, in the traditional definition, it is not straightforward to come up with an interval of possible values.
What is the difference between true error and approximation error?
True Error
The true error or true risk of a hypothesis is the probability (or proportion) that the learned hypothesis will misclassify a single randomly drawn instance from the population. The population simply means all the data taken from the world. Let’s say the hypothesis learned using the given data is used to predict whether a person suffers from a disease.
Note that this is a discrete-valued hypothesis meaning that the learned hypothesis will result in the discrete outcome (person suffers from the disease or otherwise).
- True Error = True Value – Approximate Value
Approximation Error
Oftentimes the true value is unknown to us, especially in numerical computing. In this case, we will have to quantify errors using approximate values only. When an iterative method is used, we get an approximate value at the end of each iteration. The approximate error is defined as the difference between the present approximate value and the previous approximation (i.e. the change between the iterations).
- Approximate Error (Ea ) = Present Approximation – Previous Approximation
What is the percentage error in your approximation?
Percent error is determined by the difference between the exact value and the approximate value of a quantity, divided by the exact value and then multiplied by 100 to represent it as a percentage of the exact value.
Percent error = |Approximate value – Exact Value|/Exact value * 100
What is Relative Error and how is it different from Percent Error?
The relative error is the difference between the known and measured value divided by the known value. When this is multiplied by 100 it becomes a percent error. Hence:
Relative error = |Estimated or approximate value - Exact Value|/Exact value.
Percent error = |Approximate value – Exact Value|/Exact value * 100.
What is Absolute Error and how is it different from Percent Error?
Absolute error is just the difference between the known and measured values. When it is divided by the known value and then multiplied by 100, it becomes a percent error.
Hence:
Absolute error = |Approximate value – Exact Value|
Percent error = |Approximate value – Exact Value|/Exact value * 100.
What are the uses of calculating Percent Error?
Percent error is a means to gauge how accurate and close the estimate is to the exact value of any given experiment or quantity. This method lets you determine if the collection of data is progressing in the right direction or not. It is mostly used by statistics experts and corporate companies. It is also of high importance to students who want to pursue economics.

.jpg)




.webp)

















