What is dynamic time warping?
In time series analysis, dynamic time warping (DTW) is one of the algorithms for measuring similarity between two temporal sequences, which may vary in speed. For instance, similarities in walking could be detected using dynamic time warping, even if one person was walking faster than the other, or if there were accelerations and decelerations during the course of an observation. Dynamic time warping has been applied to temporal sequences of video, audio, and graphics data — indeed, any data that can be turned into a linear sequence can be analyzed with dynamic time warping. A well known application has been automatic speech recognition, to cope with different speaking speeds. Other applications include speaker recognition and online signature recognition. It can also be used in partial shape matching applications.
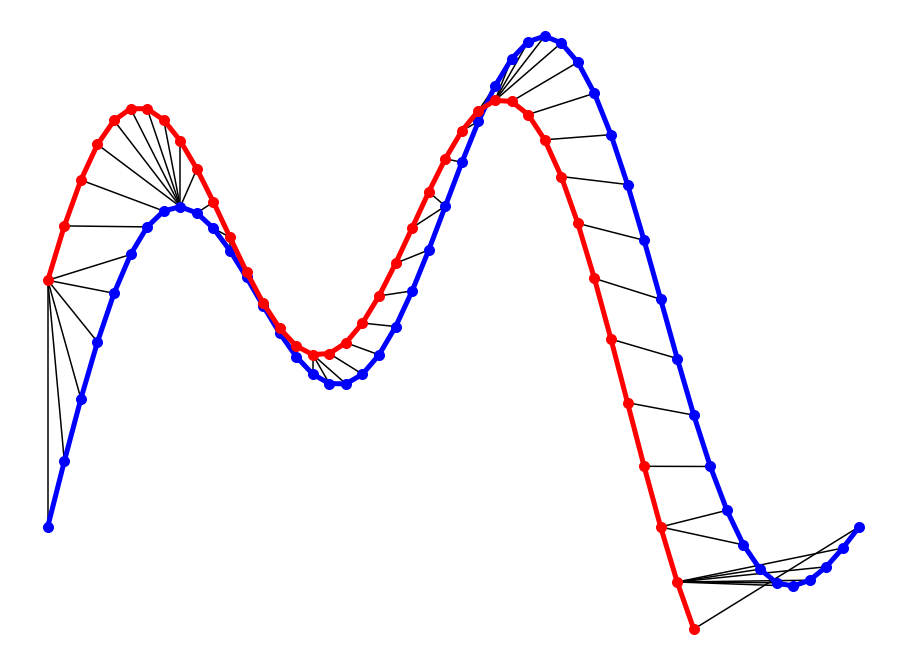
What are the rules for dynamic time warping?
In general, dynamic time warping is a method that calculates an optimal match between two given sequences (e.g. time series) with certain restriction and rules:
- Every index from the first sequence must be matched with one or more indices from the other sequence, and vice versa
- The first index from the first sequence must be matched with the first index from the other sequence (but it does not have to be its only match)
- The last index from the first sequence must be matched with the last index from the other sequence (but it does not have to be its only match)
The mapping of the indices from the first sequence to indices from the other sequence must be monotonically increasing, and vice versa, i.e. if j > i are indices from the first sequence, then there must not be two indices l > k in the other sequence, such that index i i is matched with index l and index j is matched with index k, and vice versa.
What is dynamic time warping used for?
Dynamic Time Warping is used to compare the similarity or calculate the distance between two arrays or time series with different length.
Sound Pattern Recognition
One use case is to detect the sound pattern of the same kind. Suppose we want to recognise the voice of a person by analysing his sound track, and we are able to collect his sound track of saying “Hello” in one scenario. However, people speak in the same word in different ways, what if he speaks hello in a much slower pace like “Heeeeeeelloooooo,” we will need an algorithm to match up the sound track of different lengths and be able to identify they come from the same person.
Stock Market
In a stock market, people always hope to be able to predict the future, however using general machine learning algorithms can be exhaustive, as most prediction task requires test and training set to have the same dimension of features. However, if you ever speculate in the stock market, you will know that even the same pattern of a stock can have very different length reflection on klines and indicators.
Why do we need dynamic time warping ?
Any two time series can be compared using euclidean distance or other similar distances on a one to one basis on time axis. The amplitude of first time series at time T will be compared with amplitude of second time series at time T. This will result into a very poor comparison and similarity score even if the two time series are very similar in shape but out of phase in time.
Dynamic time warping compares amplitude of first signal at time T with amplitude of second signal at time T+1 and T-1 or T+2 and T-2. This makes sure it does not give low similarity score for signals with similar shape and different phase.
How does dynamic time warping work?
Inside each cell a distance measure can be placed, comparing the corresponding elements of the two sequences. To find the best match or alignment between these two sequences one need to find a path through the grid which minimizes the total distance between them. The procedure for computing this overall distance involves finding all possible routes through the grid and for each one compute the overall distance. The overall distance is the minimum of the sum of the distances between the individual elements on the path divided by the sum of the weighting function. The weighting function is used to normalise for the path length. It is apparent that for any considerably long sequences the number of possible paths through the grid will be very large.
What are the constraints of dynamic time warping?
- Monotonic condition: the path will not turn back on itself, both the i and j indexes either stay the same or increase, they never decrease.
- Continuity condition: the path advances one step at a time. Both i and j can only increase by at most 1 on each step along the path.
- Boundary condition: the path starts at the bottom left and ends at the top right.
- Warping window condition: a good path is unlikely to wander very far from the diagonal. The distance that the path is allowed to wander is the window width.
- Slope constraint condition: The path should not be too steep or too shallow. This prevents short sequences matching too long ones. The condition is expressed as a ratio p/q where p is the number of steps allowed in the same (horizontal or vertical) direction. After p steps in the same direction is not allowed to step further in the same direction before stepping at least q time in the diagonal direction.
The foregoing constraints allow to restrict the moves that can be made from any point in the path and so limit the number of paths that need to be considered. The power of the dynamic time warping algorithm is in the fact that instead finding all possible routes through the grid which satisfy the above conditions, the dynamic time warping algorithm works by keeping track of the cost of the best path to each point in the grid. During the calculation process of the dynamic time warping grid, it is not known which path is minimum overall distance path, but this can be traced back when the end point is reached.
























