What is principal component analysis?
Principal Component Analysis (PCA) is a dimensionality-reduction technique. It enables you to reduce dimensionality by summarizing the information from large data tables with the use of a smaller set of “summary indices” which can be visualized and analyzed with greater ease.
These tinier sets still contain most of the information from the large sets of datasets. This makes it easier for machine learning algorithms to process the information, without needing to analyze extraneous variables.
It also reduces the difficulty involved in observing trends, jumps, clusters, and outliers. The summaries would even help in uncovering and understanding the relationships between observations and variables, and among the variables.
PCA pretty much is the basis of multivariate data analysis based on projection methods.
Principal Component Analysis was first formulated in statistics by Karl Pearson. He described PCA to be finding “lines and planes of closest fit to systems of points in space.”
PCA is used in the field of quantitative finance. It is applied to the risk management of interest rate derivative portfolios. It is also applied in equity portfolios, to portfolio risk as well as to risk return. It can be used to reduce portfolio risk by applying allocation strategies to principal portfolios instead of applying them to the underlying stocks. It can also be used to increase portfolio returns by employing principal components to pick stocks that have the potential to have an upside.
PCA is also used in the procedure of spike sorting in neuroscience. This involves using principal component analysis to reduce the dimensionality of the space of action potential waveforms and proceeding to carry out clustering analysis for the purpose of associating specific action potentials with individual neurons.
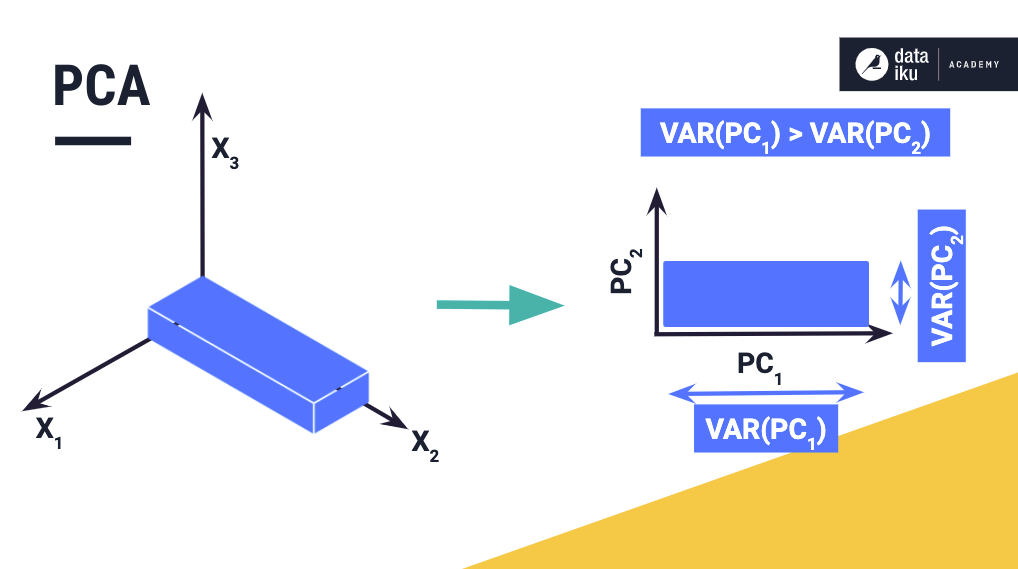
Principal component analysis reduces data by geometrically projecting them onto lower dimensions called principal components (PCs), with the aim of identifying the best summary of the data using a limited number of principal components. The first principal component is chosen to minimize the total distance between the data and their projection onto the principal component. When you minimize this distance, you also maximize the variance of the projected points. The second (and all the subsequent) principal components are selected in a similar fashion, with the additional requirement that they must be uncorrelated with all previous PCs.
The requirement of a lack of correlation means that the maximum number of principal components possible will either be the number of samples or the number of features, whichever is less. The PC selection process maximizes the correlation between data and their projection and is equivalent to performing multiple linear regression on the projected data against every variable of the original data.
Why is principal component analysis used?
The purpose of principal component analysis is to reduce dimensionality of large datasets, increase interpretability, and minimize the loss of information. To do that, it makes new uncorrelated variables that maximize variance.
Essentially, PCA simplifies the complexity in high-dimensional data by turning high-dimensional data into low-dimensional data, while still retaining patterns and trends in the data. It manages to do this by transforming the data into fewer dimensions, which act as summaries of features. High-dimensional data are rather common in biology and show up when multiple features, like the expression of several genes, are measured for each sample. This kind of data presents several challenges that principal component analysis manages to mitigate: computational expense and an increased error rate due to multiple test correction when testing each feature for association with an outcome. Principal Component Analysis is an unsupervised learning method and is actually quite similar to clustering—it identifies patterns without reference to prior knowledge about whether the samples come from different treatment groups or have phenotypic differences.
How is principal component analysis related to multivariate data analysis (MVDA)?
Principal component analysis could essentially be considered to be the mother method for multivariate data analysis (MVDA). It forms the basis of multivariate data analysis based on projection methods. This most vital use of principal component analysis is to represent a multivariate data table as smaller set of variables (summary indices) for the purpose of observing trends, jumps, clusters and outliers. This overview could help in uncovering the relationships that exist between observations and variables, and among the variables.
Principal component analysis is an extremely flexible tool and enables the analysis of datasets that may contain, for example, multicollinearity, missing values, categorical data, and imprecise measurements. The aim is to extract the critical information from the data and to express this information as a set of summary indices known as principal components.
Statistically, principal component analysis identifies lines, planes and hyper-planes in the K-dimensional space that approximate the data as well as possible in the least squares sense. A line or plane that is the least squares approximation of a set of data points makes the variance of the coordinates on the line or plane as big as possible.
What are the advantages of principal component analysis?
Here are the most significant advantages of principal component analysis:
- After your apply PCA to your dataset, there will be no correlation between your principal component, they will all be independent of each other.
- If the dimensions of the input are too high, you can increase the speed and improve the performance of an algorithm by using principal component analysis.
- PCA reduces the number of features, thus reducing overfitting.
- High-dimensional data can be transformed to low-dimensional data (2 dimensions) using PCA, which makes it easier to visualize the data.
What are the limitations of principal component analysis?
Here are the disadvantages of PCA:
- Principal components are less readable and interpretable than original features.
- If the data is not standardized before performing PCA, finding the optimal principal components will not be possible.
- If the principal components are not carefully selected, then it may miss some information that the original list of features have.
























